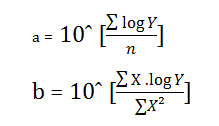DERET BERKALA PENJUALAN BERAS DARI JANUARI - MEI 2015
DAN PERAMALAN PENJUALAN BERAS JUNI - DESEMBER 2015
Hanna Qurrotul Aini (1306057)
Jurnal Statistika Dan Probabilitas
Sekolah Tinggi Teknologi
Garut
Jln. Mayos Syamsu No. 1
Jayaraga Garut 44151 Indonesia
Email :
Hannanat3@gmail.com
ABSTRAK
Deret waktu adalah
kumpulan data-data yang merupakan data historis dalam suatu periode waktu
tertentu. Data yang dapat dijadikan deret waktu harus bersifat kronologis,
artinya data harus memiliki periode waktu yang berurutan.
Beras merupakan makanan pokok orang indonesia dan
kebutuhan beras setiap harinya terus meningkat. Mekipun indonesia pernah meraih
swasembada beras namun saat ini indonesia telah melakukan import beras akibat
tingginya permintaan. Untuk membuktikannya kita dapat meramalkan dengan
menggunakan deret berkala.
Dari deret berkala tersebut dapat digunakan untuk meramalkan
jumlah penjualan beras untuk 7 bulan yang akan datang dengan menggunakan
komponen trend linear, trend kuadratis dan trend eksponensial. Berdasarkan
hasil pengamatan ketiga trend tersebut, dapat disimpulkan bahwa trend kuadratis
adalah trend terbaik untuk meramalkan kejadian dimasa yang akan datang karena
error yang dihasilkan lebih sedikit dibandingkan dengan trend yang lainnya
yaitu 17,26. Sehingga dapat diperoleh
jumlah penjualan beras dari bulan juni – desember 2015 sekitar
juni :
49 ton, juli : 58 ton, agustus : 70 ton, september : 84 ton, oktober : 101 ton,
november : 121 ton dan desember : 143 ton.
Kata
Kunci – Deret
berkala, Penduduk, Trend, Linear, Kuadratis, Eksponensial
BAB I PENDAHULUAN
1.1LATAR
BELAKANG
Deret waktu adalah
kumpulan data-data yang merupakan data historis dalam suatu periode waktu
tertentu. Data yang dapat dijadikan deret waktu harus bersifat kronologis,
artinya data harus memiliki periode waktu yang berurutan.
Deret
berkala yaitu peramalan yang didasarkan pada data kuantitatif pada masa lalu
dimana hasil ramalan yang dibuat tergantung dengan metode yang digunakan.
Apabila metode yang digunakan berbeda, maka hasil ramalan akan berbeda pula.
Metode yang baik adalah metode yang memberikan nilai perbedaan atau
penyimpangan sekecil mungkin antara ramalan dengan data yang sebenarnya.
Yang akan dibahas kali ini adalah mengenai data
penjualan beras dari januari - mei 2015 dan peramalan penjualan beras juni -
desember 2015. Mengapa ini menjadi salah satu topik yang menarik untuk dibahas
karena salah satu hal yang perlu di perhatikan oleh pemerintah adalah kerena
Beras merupakan makanan pokok orang indonesia dan semakin maraknya peredaran
baras palsu yang membuat omset penjualan beras terpengaruh.
1.2 RUMUSAN MASALAH
Berdasarkan
latar belakang penulis dalam pengamatan tersebut, dapat diambil beberapa
rumusan masalah sebagai berikut :
1. Bagaimana cara mencari data harga
beras di indonesia dalam trend linear?
2. Bagaimana
mencari data harga beras di indonesia dalam trend kuadrat?
3. Bagaimana
mencari data harga beras di indonesia dalam trend eksponen?
4. Bagaimana
memilih trend terbaik yang sesuai dengan harapan?
1.3 Tujuan
Masalah
Adapun tujuan penulisan
makalah ini, yaitu untuk mengetahui:
1. Data harga beras
di indonesia dalam trend linear
2. Data harga beras
di indonesia dalam trend kuadrat
3. Data harga beras
di indonesia dalam trend eksponen
4. Memilih trend
terbaik yang sesuai dengan harapan
BAB II LANDASAN
TEORI
2.1
PENGERTIAN DERET BERKALA
Deret
berkala merupakan kumpulan-kumpulan data berdasarkan hasil ramalan yang disusun
atas pola hubungan antara variabel yang dicari dengan variabel waktu yang
mempengaruhinya. Peramalan masa depan tersebut dilakukan berdasarkan nilai masa
lalu dari suatu variabel. Manfaat data berkala adalah mengetahui kondisi masa
mendatang. Peramalan kondisi mendatang bermanfaat untuk perencanaan produksi,
pemasaran, keuangan dan bidang lainnya. Syarat suatu peramalan kuantitatif
harus bisa memenuhi tiga kondisi yaitu tersedia informasi masa lalu, informasi
dapat dikuantitatifkan ke dalam bentuk data numerik serta dapat diasumsikan
bahwa pola masa lalu akan berlanjut pada masa yang akan datang.
2.2
KOMPONEN – KOMPONEN DERET BERKALA
Pola gerakan runtut waktu atau deret berkala dapat
dikelompokan kedalam 4 (empat) pola pokok. Pola ini bisanya disebut
sebagai komponen dari deret berkala (runtut waktu). Empat komponen
deret berkala itu adalah:
1.
Trend
(T)
Trend
(atau trend sekuler) adalah gerakan berjangka panjang yang menunjukkan adanya
kecenderungan kenaikan dan penurunan secara keseluruhan.
2.
Seasonal (S)
Komponen
seasonal atau musiman juga merupakan fluktuasi periodik, tetapi periode
waktunya sangat singkat yaitu satu tahun atau kurang.
3.
Cyclical (C)
Komponen
siklikal adalah fluktuasi pada time series yang berulang sepanjang waktu,
dengan periode lebih dari satu tahun antara satu puncak (peak) ke puncak
berikutnya.
4.
Irregular
(I)
Komponen
ini memperlihatkan fluktuasi yang random atau “noise” sebagai akibat adanya
suatu perubahan yang mendadak. Variasi random ini dapat menyulitkan kita dalam
mengidentifikasi efek dari komponen yang lain (trend, siklus, dan musim).
2.3
TREND (T) ATAU TREND SEKULER
Perkembangan suatu kejadian, gejala
atau variabel yang mengikuti “gerakan trend sekuler” dapat disajikan dalam
bentuk : Persamaan trend, baik persamaan linear maupun persamaan non linear dan
gambar/grafik yang dikenal dengan garis/kurva trend, baik garis lurus maupun
lengkung.
1. Trend
Linear
Penentuan
persamaan dan garis “trend linear” dapat dilakukan dengan metode-metode berikut
:
a. Metoda
tangan bebas (freehand method)
b. Metoda
setengah rata-rata (semi average method)
c. Metoda
matematis
d. Metoda
kuadrat terkecil (least square method)
Sering
kali data deret waktu jika digambarkan ke dalam plot mendekati garis lurus.
Deret waktu seperti inilah yang termasuk dalam trend linier. Persamaan trend linier adalah sebagai
berikut: Y’ = a + bx, dengan ketentuan a, b sebagai berikut :
Keterangan
:
Y’ =
data berkala / taksiran nilai trend
Y =
nilai variabel Y pada suatu waktu
tertentu
a = perpotongan antara garis trend dengan
sumbu tegak (Y)
b = kemiringan (slope) garis trend
x = periode waktu deret berkala
n =
banyaknya variabel Y pada suatu waktu
tertentu
1. Trend
Kuadratis
Untuk
jangka waktu pendek, kemungkinan trend tidak bersifat linear. Metode kuadratis
adalah contoh metode nonlinear.
Persamaan
untuk trend kuadratik adalah: Y’ = a +
bx + cx2, dengan ketentuan a, b, c sebagai berikut :
1. Trend
Eksponensial
Untuk
mengukur sebuah deret waktu yang mengalami kenaikan atau penurunan yang cepat
maka digunakan metode trend eksponensial. Persamaan eksponensial dinyatakan
dalam bentuk variabel waktu (X) dinyatakan sebagai pangkat. Untuk mencari nilai
a, dan b dari data Y dan X, digunakan rumus sebagai berikut: Y’ = abx
Tetapi
dalam melakukan perhitungannya, persamaan di atas dapat diubah dalam bentuk
semi log sehingga memudahkan untuk mencari nilai a dan b.
2.4
MENENTUKAN TREND TERBAIK
Untuk
membuat suatu keputusan yang akan dilakukan di masa yang akan datang
berdasarkan deret waktu diperlukan suatu metode peramalan yang paling baik
sehingga memiliki nilai kesalahan yang cenderung kecil. Terdapat beberapa cara
untuk menentukan metode peramalan mana yang akan dipilih sebagai metode
peramalan yang paling baik. Antara lain mean square error (MSE), mean absolute
error (MAE) dan mean absolute percentage error (MAPE). Berikut adalah formula
untuk MSE, MAE dan MAPE:
BAB III KERANGKA KERJA KONSEPTUAL
Adapun
kerangka kerja konseptual yang dilakukan untuk pengamatan ini adalah sebagai
berikut :
1. Menentukan topik yang akan dilakukan
didalam menentukan peramalan
2. Mengumpulkan informasi yang dibutuhkan
sesuai dengan topik tersebut
3. Menentukan kapan waktu yang akan
diramalkan
4. Menentukan komponen deret berkala yang
digunakan dalam melakukan pengamatan tersebut yaitu dengan menggunakan trend
linear, trend kuadratis dan trend eksponensial
5. Memilih trend terbaik sebagai tolak
ukur untuk memperoleh hasil peramalan yang diinginkan dimana trend terbaik
adalah trend yang jumlah errornya lebih sedikit dibandingkan dengan trend yang
lainnya.
BAB IV HASIL DAN PEMBAHASAN
1.1 Data harga beras di indonesia
januari 2014 - januari 2015
Cara pengambilan data yang dilakukan untuk menentukan
trend linear, trend kuadratis dan trend eksponensial adalah dengan mengambil
informasi dari situs litbang kompas/IWN yang disarikan dari departemen
perdagangan. Adapun data harga beras di indonesia dari januari – desember
2014 adalah sebagai berikut :
4.1 Tabel Data penjualan beras januari –
mei 2015
|
BULAN
|
JUMLAH (TON)
|
PERSENTASE
|
|
JANUARI
|
40
|
20%
|
|
FEBRUARI
|
41
|
21%
|
|
MARET
|
35
|
18%
|
|
APRIL
|
37
|
19%
|
|
MEI
|
43
|
22%
|
|
JUMLAH
|
196
|
100%
|
Dengan melihat data harga beras dari januari - mei
2015 , penulis dapat mengolahnya untuk meramalkan harga beras di indonesia
tahun berikutnya dari juni - desember 2015 dengan metode deret berkala.
1.2 TREND LINEAR
Dari data jumlah penduduk yang diperoleh, dapat
ditentukan jumlah penduduk sebagai nilai variabel Y untuk menentukan deret
berkala. Untuk mencari trend linear, penulis melakukan beberapa tahapan berikut
:
1. Menentukan nilai a dan b
Untuk
menentukan nilai a dan b, nilai-nilai yang digunakan diperoleh dari tabel
berikut :
4.2 Tabel untuk menentukan a dan b linear
|
BULAN
|
Y
|
X
|
XY
|
X2
|
|
JANUARI
|
40
|
-2
|
-80
|
4
|
|
FEBRUARI
|
41
|
-1
|
-41
|
1
|
|
MARET
|
35
|
0
|
0
|
0
|
|
APRIL
|
37
|
1
|
37
|
1
|
|
MEY
|
43
|
2
|
86
|
4
|
|
JUMLAH
|
196
|
|
2
|
10
|
Dari
tabel diatas, dapat digunakan untuk menentukan nilai a dan b dengan persamaan
sebagai berikut :
Maka trend linear untuk
nilai a dan b adalah a = 39,2 dan b = 0,2.
1.
Menentukan
Y Linear
Dari tabel 4.2 dapat pula digunakan
untuk menentukan Y linear. Adapun persamaan Y linear adalah sebagai berikut :
Y Linear = a + bx
=
39,2 + 0,2 x (-2)
=
38,8
( untuk bulan januari )
Sehingga dari persamaan tersebut, dapat
diperoleh Y linear pada tabel berikut ini :
1.1 Tabel untuk menentukan Y Linear
|
BULAN
|
Y
|
X
|
XY
|
X2
|
Y
Linier
|
|
JANUARI
|
40
|
-2
|
-80
|
4
|
38,8
|
|
FEBRUARI
|
41
|
-1
|
-41
|
1
|
39,0
|
|
MARET
|
35
|
0
|
0
|
0
|
39,2
|
|
APRIL
|
37
|
1
|
37
|
1
|
39,4
|
|
MEY
|
43
|
2
|
86
|
4
|
39,6
|
|
JUMLAH
|
196
|
|
2
|
10
|
|
2.
Menentukan
Error Linear (e linear)
Untuk persamaan error linear adalah
sebagai berikut :
E linear = ( Y – Y linear) 2
= (40– 38,8) 2
=
1,44 (
untuk tahun 2010 )
Dari persamaan tersebut, dapat
diperoleh hasil e linear pada tabel berikut ini :
1.2 Tabel untuk menentukan e Linear
|
BULAN
|
Y
|
Y
Linier
|
e
linier
|
|
JANUARI
|
40
|
38,8
|
1,44
|
|
FEBRUARI
|
41
|
39,0
|
4,00
|
|
MARET
|
35
|
39,2
|
17,64
|
|
APRIL
|
37
|
39,4
|
5,76
|
|
MEY
|
43
|
39,6
|
11,56
|
|
JUMLAH
|
196
|
|
40,40
|
4.3 TREND KUADRATIS
1.
Menentukan nilai a, b dan c
Untuk
menentukan nilai a, b dan c, nilai-nilai yang digunakan diperoleh dari tabel
berikut :
1.3 Tabel untuk menentukan a, b dan c kuadratis
|
BULAN
|
Y
|
X
|
XY
|
X2
|
X2
Y
|
X2
|
|
JANUARI
|
40
|
-2
|
-80
|
4
|
160
|
16
|
|
FEBRUARI
|
41
|
-1
|
-41
|
1
|
41
|
1
|
|
MARET
|
35
|
0
|
0
|
0
|
0
|
0
|
|
APRIL
|
37
|
1
|
37
|
1
|
37
|
1
|
|
MEY
|
43
|
2
|
86
|
4
|
172
|
16
|
|
JUMLAH
|
196
|
|
2
|
10
|
410
|
34
|
Dari
tabel diatas, dapat digunakan untuk menentukan nilai a, b dan c dengan persamaan
sebagai berikut :
Maka
trend linear untuk nilai a, b dan c adalah
a = 36,629 , b = 0,2 dan c = 1,286
1.
Menentukan
Y Kuadratis
Dari tabel 4.5 dapat pula digunakan untuk
menentukan Y kuadratis. Adapun persamaan Y kuadratis adalah sebagai berikut :
Y’ = a + bx + cx2
=
36,629 + (0,2 x -2) + 1,286 x (-2)
2
=
36,229 + 5,144
= 41,373 (untuk
januari 2015)
Sehingga dari persamaan tersebut, dapat
diperoleh Y kuadratis pada tabel berikut ini :
1.6 Tabel untuk menentukan Y Kuadratis
|
BULAN
|
Y
|
X
|
XY
|
X2
|
X2 Y
|
X2
|
y kuadratis
|
|
JANUARI
|
40
|
-2
|
-80
|
4
|
160
|
16
|
41,37
|
|
FEBRUARI
|
41
|
-1
|
-41
|
1
|
41
|
1
|
37,71
|
|
MARET
|
35
|
0
|
0
|
0
|
0
|
0
|
36,63
|
|
APRIL
|
37
|
1
|
37
|
1
|
37
|
1
|
38,11
|
|
MEY
|
43
|
2
|
86
|
4
|
172
|
16
|
42,17
|
|
JUMLAH
|
196
|
|
2
|
10
|
410
|
34
|
|
2.
Menentukan
e kuadratis
Untuk
persamaan error linear adalah sebagai berikut :
E kuadratis = ( Y – Y kuadratis) 2
= ( 40 – 41,37) 2
= 1,88
( untuk januari 2015 )
Dari persamaan tersebut, dapat
diperoleh hasil e kuadratis pada tabel berikut ini:
1.1 Tabel untuk menentukan e Kuadratis
|
BULAN
|
Y
|
y
kuadratis
|
e
kuadratis
|
|
JANUARI
|
40
|
41,37
|
1,88
|
|
FEBRUARI
|
41
|
37,71
|
10,80
|
|
MARET
|
35
|
36,63
|
2,65
|
|
APRIL
|
37
|
38,11
|
1,24
|
|
MEY
|
43
|
42,17
|
0,69
|
|
JUMLAH
|
196
|
|
17,26
|
4.3TREND
EKSPONENSIAL
1.
Menentukan
a dan b
Untuk
menentukan nilai a dan b, nilai-nilai yang digunakan diperoleh dari tabel
berikut :
1.2 Tabel untuk menentukan a dan b eksponensial
|
BULAN
|
Y
|
X
|
XY
|
X2
|
X2
Y
|
X2
|
log Y
|
X.log Y
|
|
JANUARI
|
40
|
-2
|
-80
|
4
|
160
|
16
|
1,60
|
-3,20
|
|
FEBRUARI
|
41
|
-1
|
-41
|
1
|
41
|
1
|
1,61
|
-1,61
|
|
MARET
|
35
|
0
|
0
|
0
|
0
|
0
|
1,54
|
0,00
|
|
APRIL
|
37
|
1
|
37
|
1
|
37
|
1
|
1,57
|
1,57
|
|
MEY
|
43
|
2
|
86
|
4
|
172
|
16
|
1,63
|
3,27
|
|
JUMLAH
|
196
|
|
2
|
10
|
410
|
34
|
7,96
|
0,02
|
Dari
tabel diatas, dapat digunakan untuk menentukan nilai a dan b dengan persamaan
sebagai berikut :
2. Menentukan Y Eksponensial
Dari tabel 4.7 dapat pula digunakan untuk menentukan Y eksponensial. Adapun persamaan Y eksponensial adalah sebagai berikut :
Y’ = abx
= 39,095 x 1,004-2
= 38,784 (untuk januari 2015)
Sehingga dari persamaan tersebut, dapat diperoleh Y eksponensial pada tabel berikut ini :
4.8 Tabel untuk menentukan Y Eksponensial
3. Menentukan e eksponensial
Untuk persamaan error eksponensial adalah sebagai berikut :
E eksponensial = ( Y – Y eksponensial) 2
= (40 – 38,77) 2
= 1,513 ( untuk januari 2015 )
Dari persamaan tersebut, dapat diperoleh hasil e Eksponensial pada tabel berikut ini :
4.9 Tabel untuk menentukan e Eksponensial
4.4 MEMILIH TREND TERBAIK
Dari hasil pengamatan yang dilakukan, dapat disajikan berupa grafik dari data jumlah penduduk yang sudah ada dengan menggunakan trend linear, trend kuadratis dan trend eksponensial seperti dibawah ini :
Berdasarkan trend linear, trend kuadratis dan trend eksponensial maka dapat diperoleh hasil error dari ketiga trend seperti pada tabel berikut :
4.11 Tabel untuk memilih Trend Terbaik
Dari tabel diatas, dapat diperoleh jumlah error lebih sedikit terdapat pada e kuadratis dengan jumlah 17,26. Sehingga dapat diputuskan bahwa trend kuadratis adalah sebagai trend terbaik karena jumlah errornya lebih sedikit dibandingkan dengan trend yang lainnya.
Dengan demikian, persentase jumlah penjualan beras dari bulan juni – desember 2015 dapat diramalkan sebagai berikut :
4.12 Tabel untuk peramalan jumlah penduduk Tahun 2025
Jadi, jumlah penjualan beras dari bulan juni – desember 2015 diperkirakan sekitar juni : 49 ton, juli : 58 ton, agustus : 70 ton, september : 84 ton, oktober : 101 ton, november : 121 ton dan desember : 143 ton yang diperoleh dari persamaan Y kuadratis berikut :
Y’ = a + bx + cx2
= 36,629 + (0,2 x 3) + 1,286 x (3) 2
= 37,229 + 11,574
= 48,803
= 48
Sehingga untuk perkembangan jumlah penjualan beras dari bulan juni – desember 2015 terus meningkat. Hal itu dapat dilihat seperti pada grafik berikut ini :
BAB V PENUTUP
KESIMPULAN
Berdasarkan hasil pengamatan terhadap peramalan jumlah penjualan beras dari bulan juni – desember 2015 menggunakan deret berkala dengan menentukan trend linear, trend kuadratis dan trend eksponensial, maka dapat ditarik keseimpulan bahwa trend kuadratis adalah trend terbaik yang dapat digunakan untuk meramalkan jumlah penjualan beras dari bulan juni – desember 2015. Adapun jumlah penjualan beras dari bulan juni – desember 2015 diperkirakan ada sekitar juni : 49 ton, juli : 58 ton, agustus : 70 ton, september : 84 ton, oktober : 101 ton, november : 121 ton dan desember : 143 ton.
DAFTAR PUSTAKA
http://pujiatiutari19.blogspot.com/2011/05/analisa-deret-berkala-dengan-metode.html
http://muchamadansori.blogspot.com/2014/01/analisis-data-berkala.html
statprob2014.blogspot.com